In determining the best ISO setting the term ‘Unity Gain’ pops up frequently. It refers to the ISO setting where 1 electron is converted into 1 digital value (ADU) by the Analog to Digital Converter (ADC). Intuitively it might sound appealing to use this setting and for quite a while a lot of people chose their ISO based on this value and many might still do. When we take our previous discussed description of the best ISO to use into account, this leads to basically two different scenarios and questions;
Canon users are stuck with the question whether to go beyond unity gain or not, as the typical recommended ISO will be higher than the ISO of unity gain.
Nikon users on the other hand have to deal with the question if they should stay below unity gain, as the typical recommended ISO is below unity gain ISO.
In order to get the answers to these questions we need to understand what the ‘gain’ is and what the consequences are of using different gain values.
ADC, gain and quantization error
To be able to explain gain in general and unity gain in specific, we need to introduce some new concepts here. I’ll try to be brief and explain it as clear as possible, along with examples. But of course you can always skip right to the conclusion if you want. For the people interested in this matter who want to read more than my brief description here, I’ll link to papers and posts with more detailed information, simulations and the math behind all this.
The ADC translates an analog voltage into digital bits. The voltage values are quantized (counted) in the available levels of counting; in the case of most modern cameras we are working with 14 bits and thus we have 2^14 possible levels to store a value in. For a Nikon D600 at ISO 200 the full well capacity is 38610e- which is translated into 14 bits = a range of 16384 values (2^14). The units of measurement for the analog signal is the number of electrons (e-) and for the bits this is ADU (analog-to-digital unit).
The gain of the camera is the ratio applied while converting the analog voltage signal into bits (ADUs). For the mentioned example of the Nikon D600 at ISO 200 this gain is 38610 e-/16384 ADU = 2.36 e-/ADU.
The situation where the gain is 1 e-/ADU is what often is called Unity Gain. Please note that there is no reason why a camera should have any ISO value with exactly this theoratical Unity Gain.
Since we are dealing with discrete numbers some rounding error will occur, which is known as quantization error or quantization noise. This noise is quite small; 0.29 times the Least Significant Bit (LSB).
The Lease Significant Bit is the smallest change in signal we can detect. In the case of image sensors this can be considered to be determined by the gain; if the gain is 2.36, the LSB will be 2.36 e- since that will be translated into 1 ADU. In that case the quantization noise will be 0.29 * 2.36 e- = 0.68 e-.
If you are just thinking about the signal, you might think at this point that we are throwing away faint signal by using this gain. All the pixels that will collect only 1 or 2 photons during an exposure will not be counted so it seems. So surely a gain lower than unity gain would be best?
That is a correct way of reasoning, however luckily there is a way to overcome this; adding noise. Yes that’s right; we actually want to add noise to the signal!
The benefit of noise
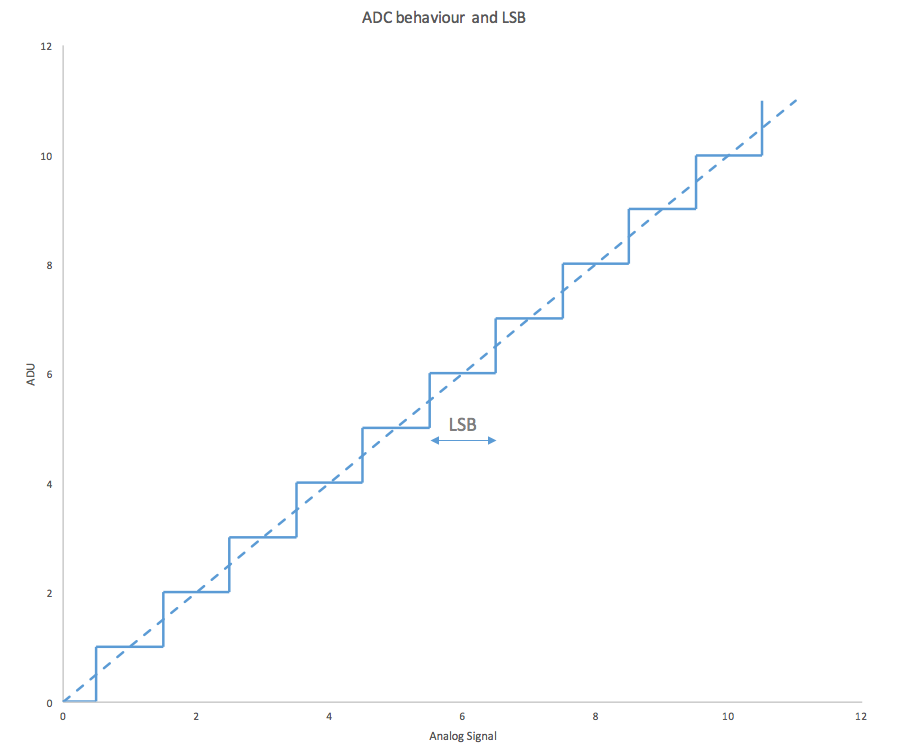
First, let’s look at the benefit the added noise has on the accuracy of the ADC. Lets consider a graph of the analog input versus the digital output of an ADC;
Since we are using discrete numbers to count and sample the analog input signal, we see a stepped slope instead of continuous. The deviation from the linear line with the stepped line at each measurement is the quantization error.
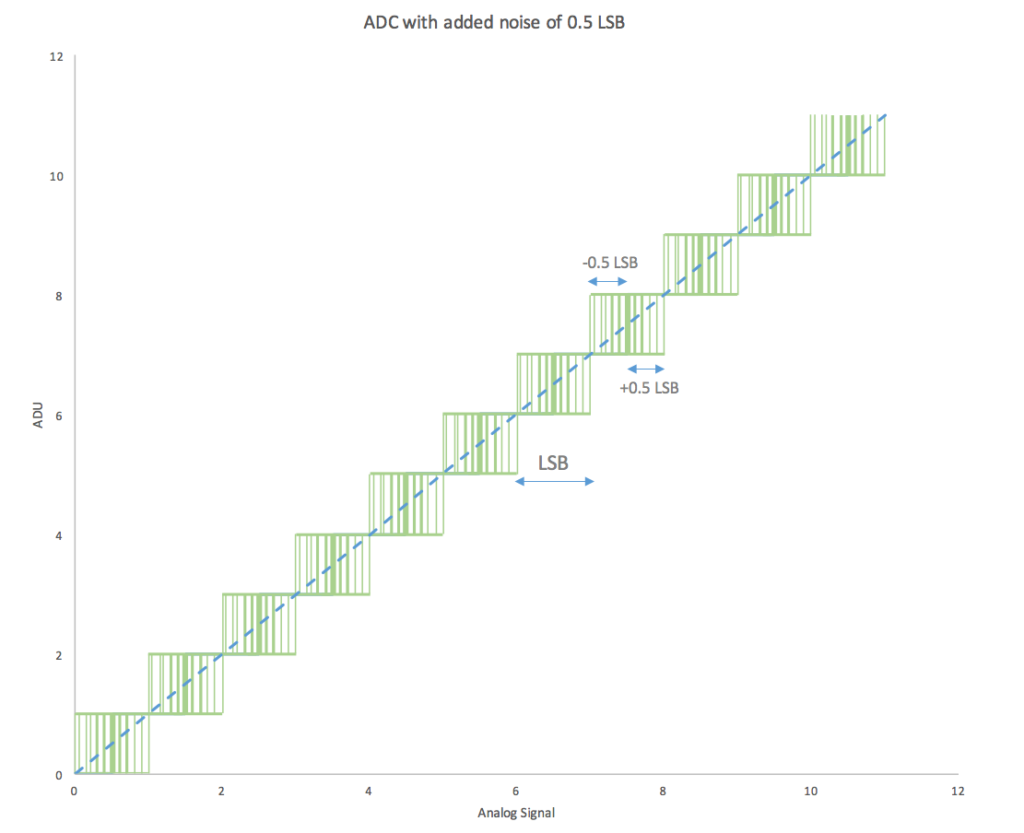
Now watch what happens when we add a noise of 0.5 LSB;
If we add noise of 0.5LSB the signal will shift (dither). This means the quantization error will behave like a Gaussian noise distribution at Sqrt (1/12) = 0.29e- This is so small that you almost never will be able to notice quantization noise in your images.
The process of adding noise to the signal is called dithering. When the ADC is sufficiently dithered it not only helps with minimizing the quantization error, it also helps acquiring faint signals smaller than 1 LSB.
When the noise exceeds 1 LSB, signal values less than 1 LSB are still properly encoded in the RAW data and can be recovered by stacking many frames.
By adding noise to the signal the ADC needs to translate, we raise the ‘floor’ of detection and prevent the < LSB values to be clipped to 0. Let’s look at the D600 at ISO 200 again; the LSB = 2.36 e-, so if we only had signal to deal with, the ADC would ‘throw away’ the signal in case we only detected 2 e-, or maybe we caught 4 e- which was rounded down to 1 ADU. When we add noise of 1 LSB, the ADC won’t see 2 e- but 5e- which would be translated to 2 ADU instead of 0. When we stack multiple frames we are able to retrieve even the signal that is below LSB. More info with examples can be found here: http://www.strollswithmydog.com/sub-bit-signal/
The noise that will always be present in our images is of course the read noise, and this will almost always be above 1 LSB. Even if it is below 1 LSB, we still have other noise sources present like shot noise and dark current noise. This means that under normal circumstances we always have noise higher than 1 LSB and we will be dithering the ADC properly for more accuracy. Considering the fact that we will be stacking multiple images when our goal is to catch the faintest of signals, the gain is also not a concern here either. Therefor we don’t need to worry about the gain in general and Unity Gain in particular.
Summary on gain and using unity gain ISO
By considering how the ADC actually works and realising that noise has a beneficial effect on the accuracy of the ADC, we now understand that gain is not a factor that we should be concerned about. So to answer the questions of the beginning of the post; there are no negative consequences for Canon users to go higher than unity gain and for Nikon users to go below unity gain. As long as we have enough noise to dither the ADC properly, we don’t loose accuracy nor sensitivity in the recovery of data.
Articles used as source and recommended readings
Wikipedia on Quantization
Wikipedia on ADC
Sub LSB Quantization
Sub Bit Signal
How read and quantizing noise interact
Read noise and quantizing, again
Noise, Dynamic Range and Bit Depth in Digital SLRs by Emil Martinec © 2008
Quantization Error in Practice

Another great article Chris! This type of technical background information is very good to have/know.
Thanks, I’m glad it is helpful 🙂
Chris, Great article. But I now have some questions … I have a Canon 6D DSLR. When I use a higher and higher ISO above Unity Gain, then I decrease the Dynamic Range. Each ISO above Unity gain, effectively cuts my Well Depth in half, resulting in more and more Pixels that are saturated / clipped at the high end. Example: The core of the Galaxy gets way over exposed / blown out. Is that not lost information? So, too high of a Gain, is a factor.
And finally, how many images must we STACK, given ALL of the noise sources, to actually recover that LSB of signal? I have stacked 32 RAW images from a Canon 6D, at ISO 800, f/7, 2 minute exposures with Histogram at 33% and yet i can clearly see noise, way above 1 LSB.
Using that type of averaging signal to noise ratio is increased by the square root of the number of images stacked (assuming they are perfectly aligned. Thus stacking 32 images will improve signal/noise by a factor of 5.65, which is about 15 dB (=20*log10(5.65)) or 2.5 bits (=log2(5.65)).
Trying to answer your question: With roughly 11 bits of dynamic range for the 6D (from the other article) in your example recovering 2.5 more bits is about 13.5 bits in total and thus close to the ADC (I expect it’s 14 bits).
One more thing to note: Depending on your processing of the RAW data your input might have been upscaled to 16 bit (or more, might even using floating point). Doing so the noise level left might be more than 2 bits, but with the full scale value increased from 2^14-1 = 16383 to 2^16-1 = 65535. So be careful and always compare your noise to the level of the lightest pixels in your image or compare the histograms as well.
I suggest anyone wondering where the sweet spot is for their camera try a night or two of practice shots at comparable exposures/iso settings. once you have a target focused and guiding, try 4x600sec shots at iso200, then without changing targets do 8x300sec at iso400 and 16x150sec at iso800 and stack all the results and see for yourself which ones you like best. For my Pentax K5(imx071) low and slow is the clear winner, just like good bbq.
Even if you push higher numbers of stack averaged data you still won’t equal the dynamic range and quality of a successful low gain long exposure guided run, but don’t take my word for it(or theirs), test for yourself.